Алгоритмы чрезвычайно важны в программировании, потому что вся компьютерная модель функционирует, когда несколько алгоритмов работают вместе. Выбор эффективного решения может быть трудным. Существует различный порядок временной сложности для определения алгоритма, из которых некоторые являются наиболее эффективными, а некоторые — наихудшими.
В блоге студии web-разработки YuSMP Group подробно рассмотрим эту непростую тему.
Что такое анализ сложности
Как определить, эффективна написанная вами программа или нет? Это измеряется сложностью.
Временная сложность алгоритма
В информатике существуют различные задачи и несколько способов решения с использованием разных алгоритмов. Они могут иметь разные подходы, некоторые из них могут быть слишком трудными для реализации, в то время как другие могут решать проблему намного проще. Трудно выбрать подходящий и эффективный вариант из всего имеющегося. Чтобы упростить выбор лучшего алгоритма, важен расчет трудоемкости и времени выполнения. Для этого проводится анализ, который определяет асимптотическую сложность.
Есть три случая, со следующими обозначениями анализа:
- Обозначение Big-oh (O) — верхняя граница времени выполнения, т. е. наихудший сценарий.
- Обозначение Big-omega (Ω) — наилучшее время выполнения.
- Обозначение Big-Theta (Θ) — среднее значение.
Как измерить сложность алгоритмов сортировки
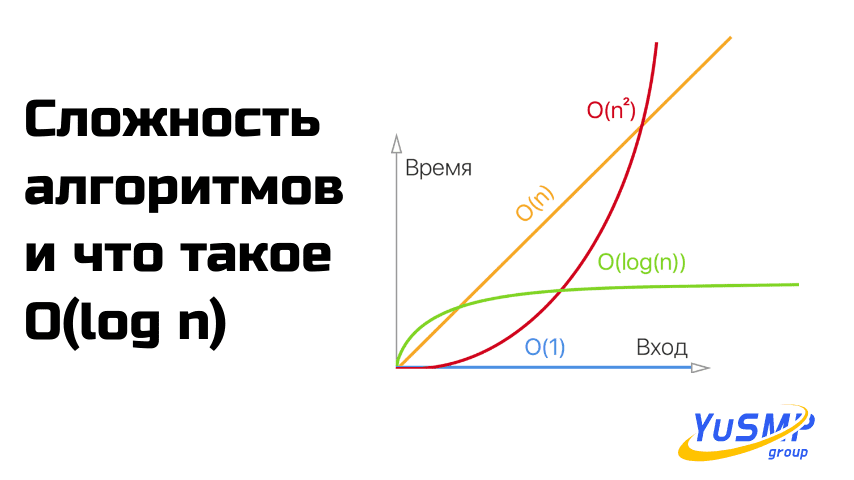
- Константа: если алгоритм выполняется одинаковое количество раз каждый раз, независимо от размера ввода. Говорят, что он демонстрирует постоянную временную сложность.
- Линейный: если время выполнения линейно пропорционально размеру входных данных, то говорят, что алгоритм демонстрирует линейную временную сложность.
- Экспоненциальный: если время выполнения зависит от входного значения, возведенного в степень, то говорят, что алгоритм демонстрирует экспоненциальную временную сложность.
- Логарифмический: когда время выполнения увеличивается очень медленно по сравнению с увеличением размера входных данных, т. е. логарифмически по размеру входных данных, говорят, что алгоритм демонстрирует логарифмическую временную сложность.
Для оценки алгоритмов используется о нотация (Большое-О).
| BIG-O | Сложность | Пример |
| O (1) | Константная | Поиск по ключу в хэш-таблице; арифметическая операция с числом |
| O (log2 (n)) | Логарифмическая | Бинарный поиск, сложность, вставка сбалансированное бинарное дерево |
| O (n) | Линейная | Поиск перебором; среднеквадратическое отклонение |
| O (n*log2(n)) | Квазилинейное | Самые быстрые алгоритмы сортировки |
| O (n2) | Квадратичная | Простые алгоритмы сортировки; перемножение n-значных чисел «столбиком» |
| O(nx) | Полиномиальная | LU-разложение матрицы; мощность графа |
| O (cn) | Экспоненциальная | Задача коммивояжёра (динамическое программирование) |
| O (n!) | Факториальная | Задача коммивояжёра перебором |
Что такое логарифм
Степень, в которую нужно возвести основание, чтобы получить заданное число, называется логарифмом этого числа по соответствующему основанию.
Для нахождения логарифма необходимо знать два фактора: основание и число.
Примеры:
Логарифм 8 по основанию 2 = log 2 (8) = 3
Объяснение: 2 3 = 8
Поскольку 2 нужно возвести в степень 3, чтобы получить 8, таким образом, логарифм 8 по основанию 2 равен 3.
Логарифм 81 по основанию 9 = log 9 (81) = 2,
Объяснение: 9 2 = 81
Поскольку 9 нужно возвести в степень 2, чтобы получить 81, Таким образом, логарифм 81 по основанию 9 равен 2.
Примечание. Экспоненциальная функция является полной противоположностью логарифмической функции. Когда значение многократно умножается, говорят, что оно растет экспоненциально, тогда как когда значение многократно делится, говорят, что оно растет логарифмически.
Что такое О(log n)
O(log N) означает, что время растет линейно, а N растет экспоненциально. Таким образом, если для вычисления 10 элементов требуется 1 секунда, для 100 нужно будет 2 секунды, для 1000 элементов — 3 и так далее.
Бинарный поиск — как раз пример алгоритма. Его структура данных — отсортированный массив из n элементов (что означает n - количество).
Другой пример — быстрая сортировка, когда каждый раз мы делим массив на две части и каждый раз требуется O(N)время, чтобы найти опорный элемент. Следовательно, это N O(log N).
Часто задаваемые вопросы (FAQ) о логарифмической временной сложности:
1) Почему логарифмическая сложность не нуждается в основании?
Логарифмы по любому основанию, т.е. 2, 10, е, можно преобразовать в любое другое основание с добавлением константы, поэтому основание логарифма не имеет значения.
2) Как логарифмы используются в реальной жизни?
В сценариях реальной жизни, таких как измерение кислотного, основного или нейтрального поведения вещества, которое описывает химическое свойство с точки зрения логарифма значения pH.
3) Является ли логарифм повторным делением?
Логарифм — это повторяющееся деление по основанию b до тех пор, пока не будет достигнуто 1. Логарифм - это количество делений на b. Повторное деление не всегда дает ровно 1.
4) В чем разница между логарифмом и алгоритмом?
Алгоритм это пошаговый процесс решения определенной проблемы, тогда как логарифм — показатель степени.
5) Почему бинарный поиск логарифмический?
Двоичный поиск — это метод поиска по принципу «разделяй и властвуй», его ключевая идея — сократить пространство поиска до половины после каждого сравнения для поиска ключа. Таким образом, пространство поиска многократно сокращается вдвое, а сложность становится логарифмической.
6) Что быстрее N или log N?
log N быстрее, чем N, поскольку значение log N меньше, чем N.
7) Что быстрее O(1) или O(log N)?
O (1) быстрее, чем O (log N), поскольку O (1) самая быстрая из возможных.
Вывод
Из приведенного выше обсуждения мы делаем вывод, что анализ очень важен для выбора подходящего алгоритма, а логарифмический порядок является одним из оптимальных порядков сложности по времени.
Эти и другие технологии веб-разработки наши специалисты используют в работе над проектами; примеры можно посмотреть в разделе кейсы YuSMP Group. Если у вас есть идея приложения или другой системы, в реализации помогут веб-услуги и разработка в YuSMP Group. Оставили контакты, чтобы вы могли связаться любым удобным способом.
No comments.