Что такое число Фибоначчи?

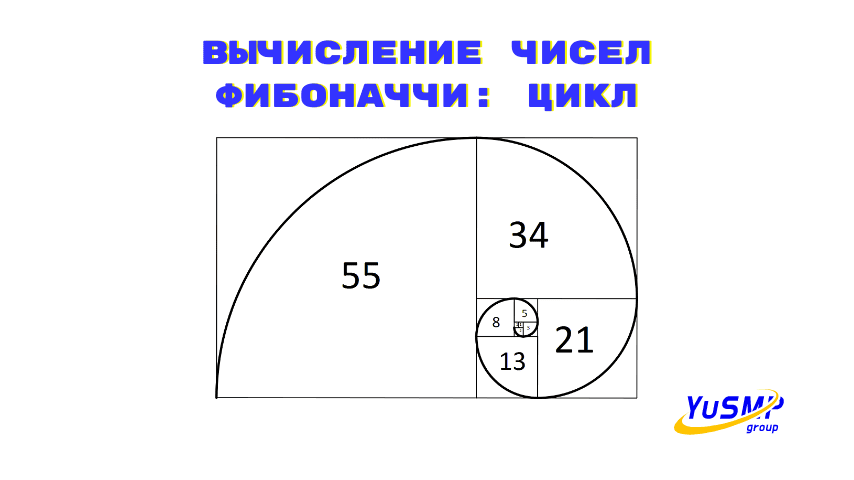
Числа Фибоначчи – это одна из самых известных последовательностей в математике. Они получаются путем сложения двух предыдущих цифр: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, и так далее. Несмотря на то, что этот ряд прост в своей форме, его свойства и связи с другими областями математики продолжают привлекать внимание ученых и любителей математики по всему миру.

Как вычислить последовательность Фибоначчи?

Теория Фибоначчи имеет много интересных свойств и применений, от графиков до финансовой аналитики. Но одним из самых основных и фундаментальных свойств этой закономерности является то, что она может быть использована для построения золотого сечения – пропорции, которая считается идеальной и гармоничной в геометрии и искусстве.

Самый простой способ найти число Фибоначчи по формуле:

F(n) = F(n-1) + F(n-2)

где F(n) - n-ое, F(n-1) - (n-1)-ое, F(n-2) - (n-2)-ое.

Например, первые несколько цифр можно вычислить по следующей формуле:

F(1) = 1

F(2) = 1

F(n) = F(n-1) + F(n-2)

Таким образом, третье равно сумме первых двух, то есть:

F(3) = F(2) + F(1) = 1 + 1 = 2

Четвертое равно сумме второго и третьего:

F(4) = F(3) + F(2) = 2 + 1 = 3

И так далее.

Также существуют более сложные алгоритмы Фибоначчи для нахождения n-го элемента, такие как формула Бине, которая использует золотое сечение, но этот способ неэффективен, так как требует вычисления больших и сложных математических операций.

Однако формула F(n) = F(n-1) + F(n-2) является самой простой и широко используется для вычисления в программировании и других областях.

Вычисление с помощью цикла

Более эффективный способ нахождения последовательности Фибоначчи – это использование цикла.

Цикл – это управляющая структура в программировании, которая позволяет повторять блок кода несколько раз, пока выполняется определенное условие. Использование такого метода для вычисления ряда Фибоначчи позволяет нам оптимизировать нахождение и значительно сократить количество операций.

Один из примеров использования выглядит следующим образом:

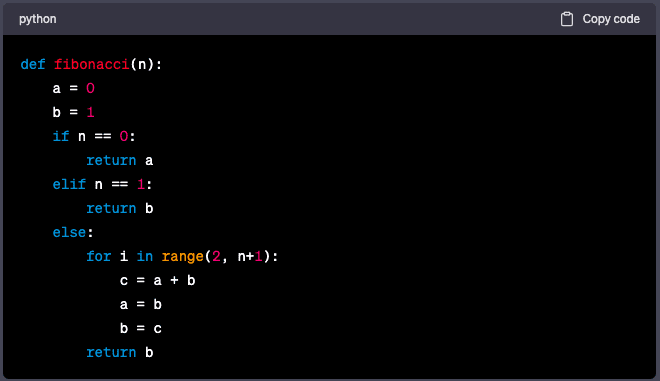
В этом примере мы начинаем с двух переменных: a и b, которые соответствуют первым двум цифрам. Затем мы используем условный оператор if для проверки, является ли введенное n равным 0 или 1. 

Если это так, мы возвращаем соответствующее значение. Если же n больше 1, мы начинаем for, который выполняется n-2 раз, так как первые два уже заданы.

Внутри программы мы вычисляем новое, сложив предыдущие два (a и b) и присваиваем результат переменной c. Затем мы обновляем значения переменных a и b так, чтобы b было равно c, а a было равно предыдущему b.

Когда программа завершается, мы возвращаем b, которая соответствует введенному n.

Одним из преимуществ использования этого способа является то, что мы можем легко находить любую цифру в ряду, а не только первые несколько. 

Например, чтобы найти девятое число Фибоначчи, мы просто вызываем функцию fibonacci(9) и получаем ответ без необходимости вычислять все предыдущие вручную.

Кроме того, использование программы может значительно ускорить вычисления по сравнению с другими методами, особенно для больших значений n. Например, если мы попытаемся вычислить 1000-е значение с помощью рекурсии, мы можем столкнуться с проблемой "слишком глубокой рекурсии", которая может привести к переполнению стека и краху. В то время как использование циклической программы позволяет избежать этой проблемы и найти искомое за доли секунды.

Также существуют многие другие интересные свойства и теории.

Например, если мы построим график Фибоначчи, мы увидим, что он имеет характерную форму золотой спирали. Эта спираль соответствует отношению: каждый следующий член является суммой двух предыдущих, и чем больше, тем ближе отношение двух соседних к золотому сечению, т.е. приблизительно 1,618.

В каких процессах в разработке используется?

• Веб-разработка: создание эффектов и макетов на веб-страницах и других платформах.
• Машинное обучение: в алгоритмах машинного обучения, таких как алгоритмы временных рядов для предсказания будущих значений, основываясь на прошлых.
• Криптография: используются в криптографии для создания ключей шифрования. 
• Анализ данных: для анализа временных рядов, таких как биржевые котировки, для выявления трендов и паттернов в данных.
• Анализ сложности алгоритмов: задачи на выявление сложности различных алгоритмов и структур данных. Например, в алгоритмах динамического программирования.
• Разработка игр: создание анимационных эффектов и спецэффектов в играх и в других продуктах.

В заключение, цифры Фибоначчи - это не только интересная математическая конструкция, но и широко применяемый алгоритм во многих областях, включая компьютерную науку и финансовые рынки. Циклы и формулы помогают находить значения, а свойства, такие как золотое сечение, представляют математическую основу для создания красивых и функциональных объектов в нашем мире.

Веб-услуги и разработка в YuSMP Group - ваш лучший выбор для реализации любого IT проекта. Проекты, которые мы создали, показывают высокие результаты доходов владельцев и являются примерами использования современных технологий. Свяжитесь с нами любым удобным способом, чтобы получить бесплатную консультацию от ведущих экспертом компании.

Больше статей ищите в блоге студии web-разработки YuSMP Group.